Simplify/Condense 1/2* log of x log of y log of z 1 2 ⋅ log(x) − log(y) log(z) 1 2 ⋅ log ( x) log ( y) log ( z) Simplify 1 2log(x) 1 2 log ( x) by moving 1 2 1 2 inside the logarithm log(x1 2) −log(y)log(z) log ( x 1 2) log ( y) log ( z) Use the quotient property of logarithms, logb (x)−logb(y) = logb( x y) log b ( xGet an answer for 'solve (yz)^log ylog z(zx)^log zlogx (xy)^log x logy solve (yz)^log ylog z(zx)^log zlogx (xy)^log x logy the dot represents multiplication sign ' and find homeworkSome more are there sigma r=1 to
Solve Y D Dx Xy X Sinx Logx Studyrankersonline
If log(x y/2)=1/2(logx logy) then find the value of x/y y/x
If log(x y/2)=1/2(logx logy) then find the value of x/y y/x- 57 views around the world You can reuse this answer Creative Commons License Ex 96, 7 For each of the differential equation given in Exercises 1 to 12, find the general solution 𝑥𝑙𝑜𝑔𝑥 𝑑𝑦/𝑑𝑥𝑦=2/𝑥 𝑙𝑜𝑔𝑥 Step 1 Put in form 𝑑𝑦/𝑑𝑥 Py = Q xlog x 𝑑𝑦/𝑑𝑥 y = 2/𝑥 log x Dividing by x log x, 𝑑𝑦/𝑑𝑥𝑦" × " 1/(𝑥 log𝑥 ) = 2/𝑥 𝑙𝑜𝑔 𝑥" × " 1/(𝑥 log𝑥 ) 𝑑𝑦




Solve The Initial Value Problem Dy Dx Y 1 X 3 Chegg Com
Log (ex 2) 18 logx y = Tan1 1 – 2 logx Tan1 4 2 log x 1 2 log x 1 – 4 (2 logx ) Y= Tan1 1Tan1 (2logx ) Tan1 4 Tan1 (2logx ) diff wrt 'x' dy/dx = 0 d2y = 0 AnswerIf a 2 and b 1 then what is the value of log a b if log 2 the value of log 80 if log102 = , what is the number of digits in 2^64 if log2= the number of digits in 5^ log 10 7Graph y = log of x2 y = log(x 2) y = log ( x 2) Find the asymptotes Tap for more steps Set the argument of the logarithm equal to zero x 2 = 0 x 2 = 0 Subtract 2 2 from both sides of the equation x = − 2 x = 2 The vertical asymptote occurs at x = − 2 x = 2
The equation 2 lo g 2 (lo g 2 x) lo g 1 / 2 lo g 2 (2 2 x ) = 1 has View solution If lo g 2 = 0 3 0 1 0 and lo g 3 = 0 4 7 7 1 , then the value of lo g 2 4 will beLog{{xy}/3}=1/2{logxlog Y} log(xy) log(3) = 1/2(log xy) log(xy) log(2) = 1/2(log xy) 2xy 4 = xy xy = 4 now x/y y logx^(1/2)/(y^5z) Use the power law first logx^(1/2) logy^5 logz If the logs are being subtracted, then the values were being divided Write as a log of a single term logx^(1/2)/(y^5z)
logx logy = 6 logx logy = 2 Now just solve as usual for logx and logy Then raise whatever base you are using (probably 10) to the respective powers 👍 The point of intersection is (10, 1/10), assuming the logarithms are in base 10 Isolate the logx in equation 1 logx = 2 logy Substitute for logx in equation 2 2 logy logy = 0 2 2logy = 0 2(1 logy) = 0 logy = 1 y = 10^1 y = 1/10 logx = 2 log(1/10) logx log(1/10) = 2 log(x/(1/10)) = 2 10x = 10^2 10x = 100 x = 10 The solution point is (10, 1/10) Hopefully this helps!X 1 , x 2 , x n and y 1 , y 2 , y n form an ascending arithmetic progression with common difference 2 and 4 respectively, then the coordinates of G in Q 1 are Medium View solution




If Log X Y 3 1 2 Logx Logy Then Find The Value Of X Y Y X Brainly In



If
Math\large\displaystyle\star/math A No Consider math\large\displaystyle\log (x y) = \large\displaystyle\log x \log y/math Put math\large if log(xy/3)=1/2(logxlogy) then find the value of x/yy/x Class 10 mathsIntermediate mathsAptitude reasoning
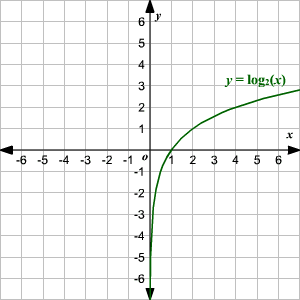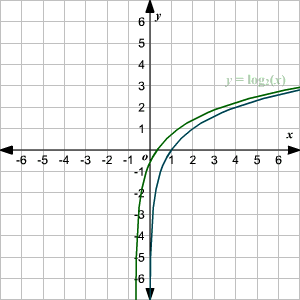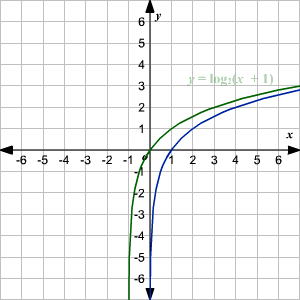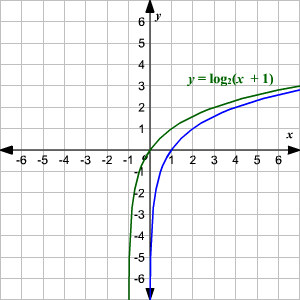



Graphing Logarithmic Functions




If Log X Y 3 1 2 Logx Logy Find The Value Of X Y Y X Class 10 Youtube
Find the value of log (a^2 / bc) log (b^2 / ac) log (c^2 / ab) ? if log x y 2 1 2 logx logy logz then find the value of x y y x Mathematics TopperLearningcom 9g3iizyy Starting early can help you score better!If the eccentricity of the hyperbola $\frac {x^2}{a^2}\frac {y^2}{b^2}=1$ is $\frac {5}{4}$ and $2x 3y 6 = 0$ is a focal chord of the hyperbola, then the



Converting Between Logarithmic And Exponential Form College Algebra



If
Click here👆to get an answer to your question ️ If sin(x y) = log(x y) , then dydx = Join / Login > 12th > Maths > Continuity and Differentiability > Logarithmic Differentiation If y = x 1 / x, the value of d x d yThe sum of 10 terms of the series whose n th terms is n 2 5 Please help Answer & Earn Cool Goodies sir this is the doubt sigma r=0 to n (r1)(nCr)^2 = ? Ex 57, 9 Find the second order derivatives of the function 〖 log〗〖 (log〖𝑥)〗 〗 Let y =〖 log〗〖 (log〖𝑥)〗 〗 Differentiating




If X 2 Y 2 7xy Then Show That 2log X Y Logx Logy 2log3



If Log X Y 2 1 2 Logx Logy Prove That X Y Brainly In
Related Searches to log xY = 100 and log x2 = 10, then the value of y is ?0 We can write the term of interest as log ( 1 x 2) = log ( 1 y 2) = ∫ y x 2 t 1 t 2 d t Now, the integrand f ( t) = 2 t 1 t 2 attains its maximum value of 1 when t = 1 Therefore, the inequality follows immediately from the mean value theorem 2 Answers2 This is because x = y = 1 is the only solution to the given equation Note that the minimum value of x log (x) is 1 and that happens when x = 1 Obviously, the same is true for y log (y) So, log (x)log (y)xy is always greater than 2 except at x = y = 1, where it is exactly equal to 2




Implicit Differentiation Advanced Example Video Khan Academy




Solve The Initial Value Problem Dy Dx Y 1 X 3 Chegg Com
Get answer If x^2y^2=27xy, then show that log((xy),(5))=1,2logxlogyIf i assumed a value 1 for y then i was able to solve for x to get x = and x = i confirmed that when x = 685 and y = 1, the original equation is true log (sqrt4(x^16 / y^4)) What is the value of the expression when logx=8 and logy=1?




If Log X Y 3 1 2 Logx Logy Then Find The Value Of X Y Y X




If X 2 Y 2 14xy And 2log K X Y Logx Logy Then The Value Of K Is Youtube
x/y =1/2(3 sqrt(5)) From 2 log(xy)=log x log y we know (xy)^2=xy Now calling x = lambda y and substituting (lambda yy)^2=lambda y^2 or supposing y > 0 (lambda1)^2=lambda Solving for lambda lambda^23lambda1 = 0 lambda = 1/2(3 pm sqrt(5)) so remembering that x > y the feasible solution is x/y =1/2(3 sqrt(5)) log (xy)/2 = 1/2 ( logx logy) log (xy) / 2 = 1/2logxy xy/2 = √xy xy = 2√xy Squaring on both sides;Rewrite in Exponential Form log of x=1/2 log(x) = 1 2 log ( x) = 1 2 For logarithmic equations, logb(x) = y log b ( x) = y is equivalent to by = x b y = x such that x > 0 x > 0, b > 0 b > 0, and b ≠ 1 b ≠ 1 In this case, b = 10 b = 10, x = x x = x, and y = 1 2 y = 1 2 b = 10 b = 10 x = x x = x




If Log X Y 3 1 2 Logx Logy Then Find The Value Ofx




Pdf Differential Equations
$\log{\Big(\dfrac{xy}{3}\Big)}$ $\,=\,$ $\dfrac{1}{2}(\log{x}\log{y})$ The left hand side expression is purely in logarithmic form but the right hand side expression is also in logarithmic form but the factor $\dfrac{1}{2}$ pulled us back in eliminating the logarithmic form from the equation10th class mathematics Mathematics, ncert, SSC, telangana board mathematics, andhra board mathematics, state syllabus, real numbers, logarithms, sets, polynYou can put this solution on YOUR website!



If Logx Logy Log X Y Thena X Y B X Y 1 C Y X 1 X D Y X X 1 Youtube




Proofs Of Logarithm Properties Chilimath
Problems Logarithms x is a literal number The product of logarithm of 2 to x and logarithm of 2 to quotient of x by 16 is equal to the logarithm of 2 to quotient of x by 64 The value of x has to be evaluated on the basis of this data The three logarithmic terms contain different bases So, it is not possible to simply it easilyIf 10^ = 2, then find the value of log0125 (125) ? Consider the function y = x^x √x 1Express the above function as logy = (x 1/2)logx 2 Find dy/dx asked Jan 23 in Continuity and Differentiability by Raaida ( 297k points)



Log Rules Logarithm Rules



5 Derivative Of The Logarithmic Function
My work x=10^8 y=10 I tried to plug these in but my calculator but it said "overflow" Is there an easier way to do this?Click here👆to get an answer to your question ️ If log ( x y3 ) = 12 (logx logy) , then find the value of xy yxCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history



Solve Y D Dx Xy X Sinx Logx Studyrankersonline




If Log X Y 3 1 2 Logx Logy Then Find The Value Of X Y Y X
Ch 1 Real Numbers, Exercise 156 If log(xy)/3 = 1/2 (logxlogy),find the value of x/yy/x AP SCERT Mathematics Textbook, Pg 23CCE MODEL, AP/TG Class 10Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more If log (xy/5)=1/2 (logxlogy) find the value of x/yy/x ashish supplies bread and jams to a hospital and a schoolbread and jam are sypplied in equal number of pieces bread comes in a bunch of 8 pieces and




Log X Y 3 1 2 Log X Log Y Show That X Power 2 Y Power 2 11xy Brainly In




Given Math 2 Log X Y Log X Log Y 2 Log 3 Math Show That Math X 2 Y 2 7xy Math Quora
To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW If log x logy log z = (yz) (zx) (xy), thenIf x 1 = a, y 2 = b;Get answer If x^2y^2=7xy, then prove that log((xy),(3))=1,2(logxlogy)




Log X Y Logx Logy Then X Scholr



If Log X Y X Y What Is Dy Dx Quora
If 1, logy x, logz y, 15 logx z are in AP, then (A) z3=y1=x (B) x=y2 2y=z3 (D) x=y2=z4 Check Answer and Solution for above question fromClick here👆to get an answer to your question ️ If x^2 y^2 = 25xy, then prove that 2log(x y) = 3log3 logx logyradg8 and 125 more users found this answer helpful




Log X Y 7 1 2 Logx Logy Brainly In




If Log X Y 5 1 2 Logx 1 2 Logy Show That X 2 Y2 27xy Brainly In
X²y²2xy =4xy x²y² = 6xy Hence proved !Mathlogx / log5 = log36 / log6 = log64 / logy/math We know that, mathloga / logb=log_b a/math Now our original equation becomes, mathlog_5 x = log_6 36Maths Solve simultaneous equation log2(x14y)=3 logxlog(y1)=1



Show That



2




Sat Ii Math Level 2 Test 04 Solution 1 If F Is A Linear Function And F 3 7 F 5 1 And F X 11 2 What Is The Value Of X A 3 2 B Ppt Download



If X Y E X Y Show That Dy Dx Logx Log Xe 2 Sarthaks Econnect Largest Online Education Community



2



How To Solve Log X Log Y Quora



2




Ax If Y Ax Prove That Dy Dx Y2 Log Y X 1 Y Logx Logy Explain In Great Detail Mathematics Topperlearning Com Yfelkwrr




Ipe Material Notes



If F X Cos Logx Then F X F Y 1 2 F X Y F Xy Youtube




If Log X Y 2 1 2 Log X Log Y Prove That X 2 Y 2 6xy Brainly In




Properties Of Logarithms Algebra Ii Quiz Quizizz




If Log X Y 3 1 2 Logx Logy Then Find The Value Of X Y Y X Brainly In



If X 2 Y 2 7xy How Do You Prove That 1 2 Logx Logy Log X Y 3 2 Quora




If Log X Y 6 1 2 Logx Logy Show That X Y Y X 34 Brainly In



Indices And Logarithms




If Log Y X Log X Y 2 X 2 Y 12 Then The Value Of X



If U Log X 2 Y 2 Xy Then X U X Y U Y Is A 0 B U C 2u Sarthaks Econnect Largest Online Education Community



Search Q If Log X 2by 2 3d1 2 Logx 2blogy Show That X 3dy Tbm Isch



Proof Of Log Xy Log X Log Y Mathematics Stack Exchange




If X 2 Y 2 7xy Then Show That 2log X Y Log X Log Y 2log 3




If Log X Y 3 1 2 Logx Logy Then Find The Value Of X Y Y X




If X And Y Are Real Numbers Such That 2log 2y 3x Logx Logy Th




Applied Numerical Methods Question Bank




If Log X Y Log 2 1 2logx 1 2 Logy Then Youtube




Logarithmic Equations Variable In The Base Video Khan Academy




If Xy Log X Y 1 Prove That Dydx Y X 2y X Y X Xy 2 X Y




Ex 9 6 7 Find General Solution X Log X Dy Dx Y 2 X Log X



Understanding Log Plots Course Wiki



Introduction To Logarithmic Functions




Ex 9 4 16 For Xy Dy Dx X 2 Y 2 Find Solution




Engineering Mathematics Notes




If Log X Y 5 1 2 Log X Log Y Show That X 2 Y 2 27 Xy Brainly In




Ex 9 6 7 Find General Solution X Log X Dy Dx Y 2 X Log X
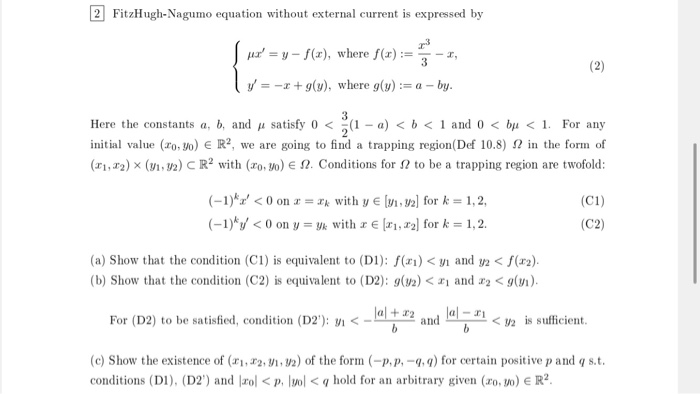



2 Fitzhugh Nagumo Equation Without External Current Chegg Com




Rewrite The Following Expressions As A Single Chegg Com



If X Y Y X What Is Dy Dx Quora



If Log Y 2log 3x 1 1 How Do You Express Y In Terms Of X Quora




Ex 5 5 15 Find Dy Dx Of Xy E X Y Class 12 Ex 5 5



Proof Of Log Xy Log X Log Y Mathematics Stack Exchange



Let X And Y Be Two Real Numbers Such That 2ln X 2y Log X Log Y What Is The Possible Value Of X Y Quora




Engineering Mathematics Notes



5 Derivative Of The Logarithmic Function
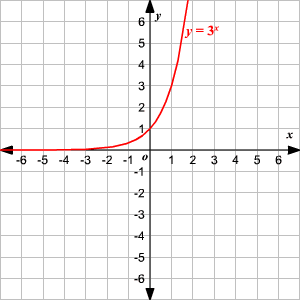



Graphing Logarithmic Functions
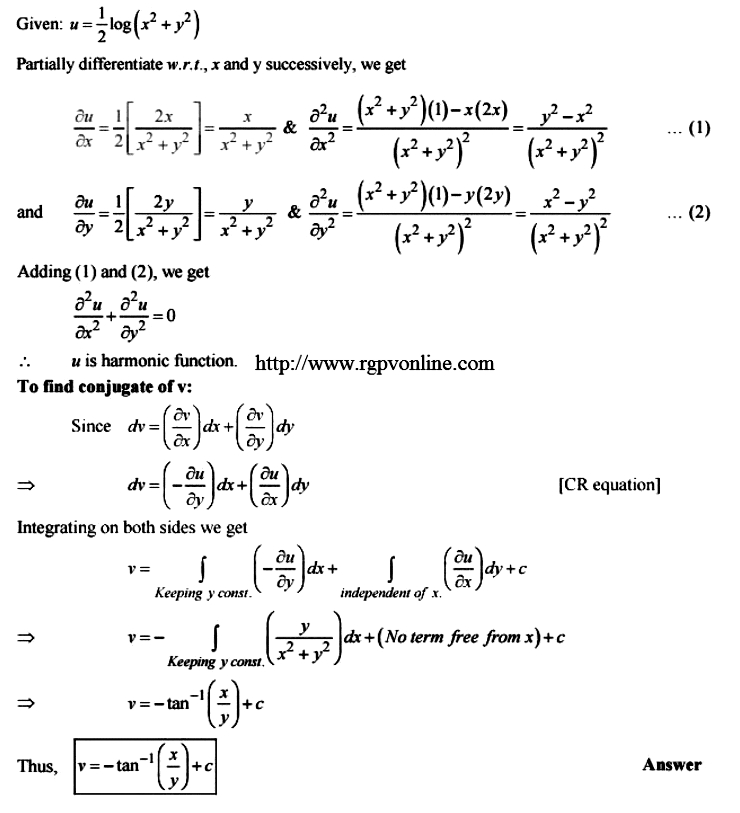



Show That The Following Function U 1 2 Log X 2 Y 2 Is Harmonic And Find Its Harmonic Conjugate Functions Mathematics 2 Question Answer Collection




X Y Dx Dy 0 Novocom Top




If Log X Y 6 1 2 Logx Logy Show That X Y




Logarithmic Mean Wikipedia



2




If Log X Y Z Logy Z X Logz X Y Then Prove That X




Log X Y 3 1 2 Log X Logy Find The Value Of X Y Y X Brainly In
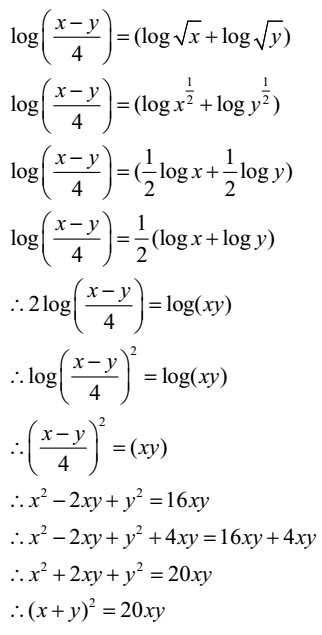



Rules Of Logarithms Archives The Fact Factor




If Log X Y 3 1 2 Logx Logy Then Find The Value Of X Y Y X



Solve X Dy Dx Y Log Y Log X 1 Studyrankersonline




Engineering Mathematics Notes
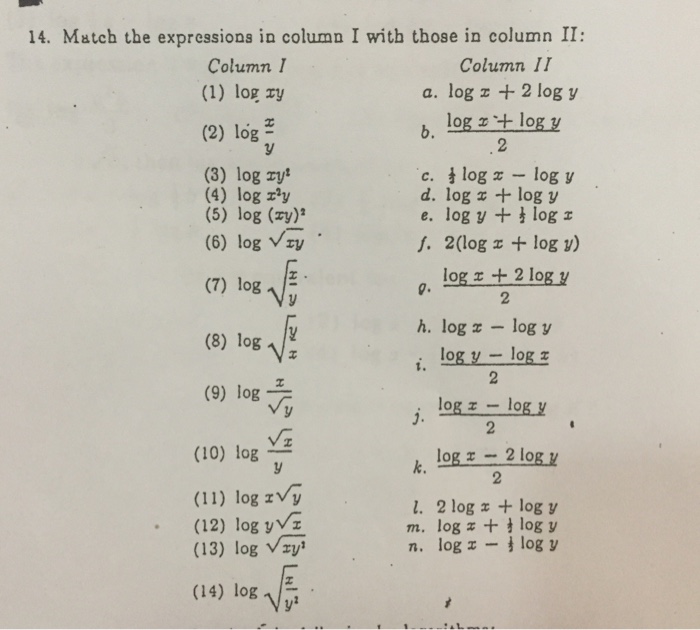



Match The Expressions In Column I With Those In Chegg Com
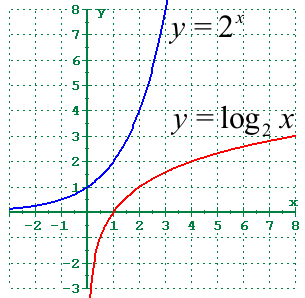



4 2 Logarithmic Functions And Their Graphs




Engineering Mathematics Notes




Log Log Plot Wikipedia




If X And Y Are Positive Real Numbers Such That 2log 2y 3x



2




If 2log Log X Y 5 Logx Logyshow That X Y Y X 27 Brainly In
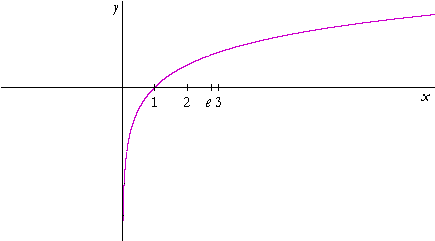



Logarithmic And Exponential Functions Topics In Precalculus




Implicit And Logarithmic Differentiation




If Log X Y 2 1 2 Logx Logy Logz Then Find The Value Of X Y Y X Mathematics Topperlearning Com 9g3iizyy




If Logx Logy Log X Y Then A X Y B X Y 1 C Y X 1 X D




Class 10 Real Numbers Mathematics If X2 Y2 25xy Then Prove 2log X Y 3log3 Log X Log Y Youtube




Log X Y Logx Logy Then X Scholr




If Log Y X Log X Y 2 X 2 Y 12 The Value Of X Y Is 9




X 3 Y 3 0 Prove That Log X Y 1 2 Logx Logy Log3 Brainly In




If X Y Log X Y 1 Prove That Dy Dx Y X 2y X Y X X Y




Ml Aggarwal Solutions For Class 9 Chapter 9 Logarithms Get Free Pdf




If Log X 2 Y 2 Tan 1 Yx Then Prove That Dydx X Yx Y



2




If Log X Y 3 1 2 Log X Log Y Then Find The Value Of X Y Y X In Telugu Youtube




Series Expansion Of Exponential And Logarithmic Functions
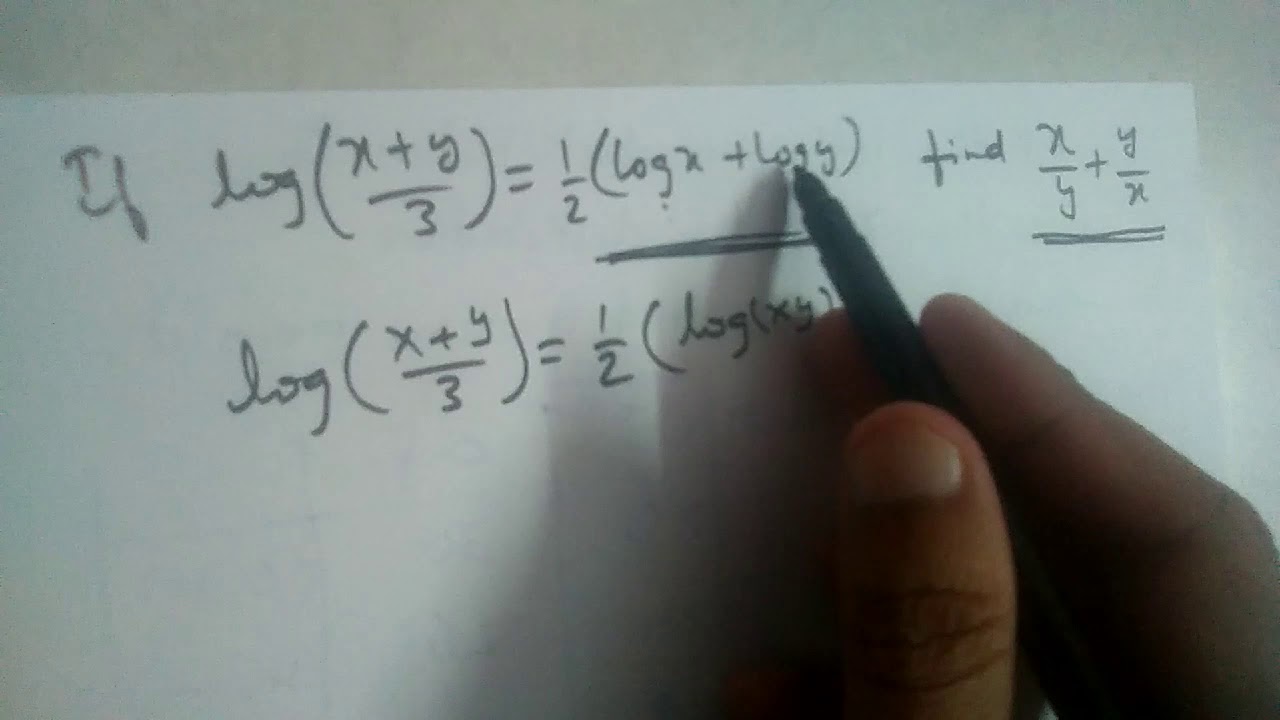



If Log X Y 3 1 2 Logx Logy Find The Value Of X Y Y X Youtube




Log X Y 5 1 2 Log X Log Y Show That X Y Y X 23 Brainly In



0 件のコメント:
コメントを投稿